Joint Mathematics Meetings January 2011

The 2011 Joint Math Meetings started for me with the advisory board meeting of the Mathematical Sciences Digital Library (MathDL). Both the MAA Reviews and the Classroom Capsules are currently free on the MathDL site to both MAA members and non-members.  The Reviews are useful mainly to faculty and libraries making decisions about purchasing books, but the "Classroom Capsules and Notes brings together the best of 114 years of the short classroom materials from the MAA print publications" and should be of use to all math faculty.

The MAA now hosts WeBWorK, an open source (free) web-based homework system originally out of Rochester U.  If your institution is unable or unwilling to host WeBWorK on its own server, the MAA will let you try out WeBWorK with up to 100 students from your school.  (And if you want to try it out with more students, ask anyway, and the MAA will try to find a participating institution that can accommodate you.)

Aaron Wangberg of Winona State U. has created an electronic whiteboard to work within WeBWorK.  His students are required to use the whiteboard to show their work before submitting their answers for the instant correct/incorrect feedback.  Mike Gage says this utility will soon be available to all the WeBWorK authoring community.

Warren Esty of Montana State U:  Theorem  The value of math skills has gone way down.  Corollary  We should focus our teaching toward skills that will add value.  Examples:  Being able to read math and to make the right things "come to mind."  (The idea of the latter example is that information and computation are both cheap, but knowing what is relevant to look up or to compute is harder to come by.)

At the CTiME sponsored panel session on the final day I learned a bit more about MathJAX, which is rapidly becoming the standard tool for putting math notation on the Web.  MathJAX is largely the work of Davide Cervone of Union College.

Much of the excitement about MathJAX is that it provides a much needed piece of the puzzle so that the potential of MathML can be realized.  Although MathML has been the World Wide Web Consortium (W3C) standard for putting math on the Web for 15 years, it has not been widely accepted by browsers.  MathJAX allows the author of a webpage to use TeX or MathML to specify math notation, and MathJAX instructs the browser how to display the math properly, even for browsers that do not know how to display MathML.

Steve Wilson (AMATYC Central Vice-President) told me that he spent a few hours in the exhibits room.  Besides the major textbook publishers and mathematical software providers, the exhibitors at JMM 2011 included WeUseMath.org, which showcases information and resources for students and faculty about careers, etc.  The ALEKS rep would give me no numbers at all about possible costs, but the WebAssign folks were happy to chat about costs or anything else.

One American Mathematical Society booth freebie was a report on an AMS survey about online homework systems.  By far the most frequently adopted were 1) MyMathLab, 2) WebAssign, and 3) WeBWork.  MML involved the most students (230K), then WeBWorK with over 100,000 and WebAssign with less than 100,000.  There was no effort to rate the relative quality of the different homework systems, but I found it interesting that the study divided the PhD granting institutions into those that were among the top 80 (as ranked by the National Research Council) and those ranking below the top 80.  For example, the response rate among the top 80 was 71%, for the rest of the PhD-granting universities the response rate was 65%.  For the masters-granting universities the response rate was 45%, for bachelor's 30%.  "The two-year college numbers were too small for any meaningful analysis" as "Only 11 responded" of the 30 TYC invited to participate.

Gaps in developmental math students' knowledge

The Pierce College Modular Math 115 project for a modular, self-paced, mastery-based elementary algebra course is in its third semester.

We've made adjustments each semester.  This semester we've used the open source online homework system WeBWorK so that students can verify that they have the correct answers on all the drill questions, so we no longer collect those homework sets on a daily basis.

This semester we are acknowledging how inadequately we have met the self-paced aspect of the plan.  The four sections of Modular Math 115 all meet at the same hour so that we can physically relocate students to the classroom that is progressing at the pace most appropriate for them.   In order to accommodate students who cannot master our elementary algebra materials within one semester, we are moving the slower students (electronically) to a course in the district database that covers only the first half of a two-semester elementary algebra course.

Among the 43 students in my classroom, none had mastered even two (of the nine total) units by the end of the twelfth week of fifteen weeks in the semester.

The students suffer all the mathematical gaps we have come to expect, such as inability to distinguish the concepts of area and perimeter.  But I was surprised by how many of the students have only a very shallow understanding of subtraction (and of course of multiplication and division).

They are all capable of computing 5 - 3.  And they can easily answer, "If you had 5 pencils and I took away 3, how many pencils would you still have?"

That particular word problem involves the simplest model for subtraction, "take away".  But my students have trouble with the more sophisticated, "If your pencil box holds 5 pencils and you already have 3, how many more pencils do you need to fill the pencil box?" 

The students do not automatically recognize their task as computing a difference.  Instead, they solve such a problem by counting up from 3, and so they have even more trouble with "If you had some pencils and then I gave you three more so that you had a total of 5 pencils, how many pencils did you have at the start?"

And they have more difficulty with a comparison question, "If you have 3 pencils and I have 5, how many more pencils do I have than you?"

Some of the students seems unfamiliar with the idea of multiplication as repeated addition--they know some multiplication facts but do not recognize that one can compute 3+3+3+3 by multiplying 4*3. 

Even if we assume that our students have access to technology to carry out computations and symbolic manipulations, some of these students do not recognize what calculation or manipulation is useful when given a context outside of pure mathematical computation.

Rope-stretching a right corner

A colleague asked today if one could find positive integers a, b, c, and d so that a² + b² + c² = d², or if that was an open problem.  He added that he'd heard that Egyptians stretched ropes to create 3-4-5 triangles in order to form right angles, and was wondering about the possibility of a three-dimensional analog.

I mentioned the Google Group investigating the harder problem of finding a rectangular box with integer sides, integer diagonals, and integer main diagonal.  (See http://groups.google.com/group/theperfectcuboid?lnk=iggc.)

But only while driving home did it occur to me that it's straightforward to produce lots of examples of my colleague's easier problem.

Start with your favorite primitive Pythagorean triple (a, b, c).  (See my earlier post about Pythagorean triples:  http://byoshiwara.blogspot.com/2009/12/blog-post.html.)

Then c is odd, so c = 2n + 1, and

a² + b² + [2n(n + 1)]² = [2n(n + 1) + 1]²

For example, 3² + 4² + 12² = 13².

A short wish list for online homework systems

I take it for granted that electronic homework systems cannot effectively grade any math problem that requires students to write coherent sentences.

All the electronic homework systems allow the possibility of students submitting answers that won't be machine graded.  This capability greatly increases the variety of types of questions that can appear in an electronic exercise set.  There is an issue of how students enter math notation and figures (hey, just let them  photograph their handwritten answers with their cellphones and upload the jpg file), but the principal reason that I'm reluctant to include such problems is the fear that grading online will be cumbersome.

There are several ways to make life easier for the instructor faced with grading a single "essay" problem from a large set of students.  First, the interface for viewing individual responses should be intuitive and effortless.  Don't make us click on a link to open one student's response and then have to close that file before opening the next. 

It would be better to have "zoomable" thumbnails of each student's answers spread across the screen, with mouse flicks or dragging to scroll.  Should the instructor have the foresight to provide a grading rubric for the problem, that rubric should be visible (or at least available) to the student when working the problem.

In many cases, the availability of the rubric could reduce the instructor's need for to make copious comments.  For further convenience, the instructor should have a few editable paste buffers holding common comments (like "You need the product rule" or "This is not an equation").

A joyful conspiracy

Uri Treisman's Joyful Conspiracy from CarnegieViews on Vimeo.

The Carnegie Foundation for the Advancement of Teaching is organizing a “joyful conspiracy” to help community colleges provide pathways to success for students who initially are placed in developmental mathematics courses.  The Statway will bring non-STEM students from the level of elementary algebra up to and through a transfer-level statistics course in one year.

The Statway 2010 Summer Institute brought teams from 19 community college campuses to the Stanford University campus July 25-30 to meet, share with, and learn from each other and from Carnegie Foundation leaders and consultants.  

We practiced the protocol for presenting, critiquing, and giving feedback on the lessons we will be piloting in the coming year.  Each lesson will involve students working on a rich task with clearly defined learning goals.  A key assumption of Statway is that statistics can provide a context for students to learn to think and reason quantitatively.  The necessary algebraic skills will be embedded within the lesson, rather than holding center stage.

Another core part of the instructional experience is that having students struggle with problems is desirable.  This student engagement, even when students do not discover or invent the necessary mathematics on their own, can be crucial to preparing the students for making sense of the central topic of the lesson.

Statway lesson protocol

Thursday afternoon and Friday morning (July 8 – 9, 2010) Pierce College math faculty Vic LaForest, Bob Martinez, Kathy Yoshiwara, and I were in a “fishbowl” as part of the development of the Statway project.

In the coming year, faculty teams from 19 community college campuses will take materials (developed by the Carnegie Foundation for Advancement of Teaching) and create, test, analyze effectiveness of, and give feedback on statistics lessons. The purpose of our two-day experience was to test out a protocol developed for carrying out this process.

The lead facilitator was Bill Saunders, formerly of Pearson Learning Teams. He was joined by UCLA research colleagues Jim Stigler and Karen McGivven, Kris Bishop of the Dana Center (UT Austen), and Alicia Grunow of Carnegie.

We were not allowed to see the proto-lesson until we met Thursday. After a brief introduction to the protocol and the Statway lesson approaches, we four faculty members spent much of the afternoon working among ourselves deciding how we could best implement that lesson, while a video camera and the observers watched on.

We were expected to have the lesson design completed before our 5:30 pm adjournment Thursday. Bob was chosen to deliver the lesson at the start of the Friday session, and Karen volunteered to acquire the materials needed for our modified lesson. Kathy and I agreed to put together and email some of the materials Bob would need for his handouts.

Bob was working until 2:00 am putting together the materials.

Our Pierce College deans Jacquinita Rose and Crystal Kiekel were attending as guests. But when only 3 students showed up from the 8 students that had been recruited for Friday morning, we put Crystal and Alicia to work, enlisting them to act as students for Bob's lesson.

Bob did a great job running the lesson. After the students departed with their $20 iTunes gift cards, we continued the lesson protocol with the debriefing of how the lesson went, analyzing the student work, and writing feedback on the lesson.

The researchers were pleased with how everything went, and promised we would not be seeing the videos on YouTube.

Variance in values from prediction by regression

In a section about linear regression in Understanding Statistics in the Behavioral Sciences (7th), Robert Pagano, Thomson, 2004, we find the following equation on page 119.

After an explanation of the notation, we find,

We could then construct for each score.  If we squared each and summed over all the scores, we would obtain

Obtaining this second equation from the first seems remarkable, but the textbook offered no insights on how one could see this.

Here's one possibility.

If we think of vectors , , and , then the second equation above is the assertion that

This equation is true whenever the vectors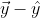 and 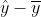are orthogonal.

But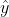 is precisely the orthogonal projection of 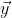onto the space spanned by and (see my earlier blog), so 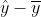is in that space and 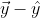is in the orthogonal complement.