In a section about linear regression in
Understanding Statistics in the Behavioral Sciences (7th), Robert Pagano, Thomson, 2004, we find the following equation on page 119.
After an explanation of the notation, we find,
We could then construct 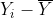 for each score. If we squared each
for each score. If we squared each 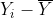 and summed over all the scores, we would obtain
and summed over all the scores, we would obtain
Obtaining this second equation from the first seems remarkable, but the textbook offered no insights on how one could see this.
Here's one possibility.
If we think of vectors
)
,
)
, and
)
, then the second equation above is the assertion that
This equation is true whenever the vectors
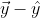
and
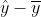
are orthogonal.
But
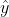
is precisely the orthogonal projection of
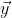
onto the space spanned by
)
and
)
(
see my earlier blog), so
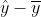
is in that space and
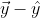
is in the orthogonal complement.
for each score. If we squared each
and summed over all the scores, we would obtain


No comments:
Post a Comment